×

I have been a heavy user of the sigmoidal 4-parameter logistic regression (abbrv. sigmoidal 4PL) function since graduate school, some time around 2018 when I was on my second lab rotation. Sadly, I never thought much about it until Friday last week (2024/DEC/20), 6 years later. Aside from appreciating its beauty and its closer relationship to biology^[1], I never engaged with it deeply.

... and today I decided to play with it.

Half-Maximal

Sigmoidal 4PL is a parametric equation with 4 components, often used to model the behavior of drug concentration (the dose) and its resulting biological phenomenon (the response), earning the moniker dose-response curve. Sigmoidal 4PL understands the slope (a.k.a. Hill's slope^[2]), the midpoint (a.k.a. the inflection point), the maximum value, and the minimum value. Three components are often ignored^[3], while the midpoint receives an outsized attention. In literature, the midpoint denotes the efficacy of a drug. It used to be reported as half-maximal concentration, but the field has come up with several terms such as median inhibitory concentration (IC₅₀), or median effective concentration (EC₅₀), or median effective dose (ED₅₀). Their usage depends on their context and sometimes at the whims of the experimenter.

Last Friday, as I helped a trainee to plot for antibody-mediated neutralization of viral infectivity, I anticipated her to ask me why the field ended up using the median concentration to report antibody's activity. She did not. The thought sat with me for several hours because I realized I had no intuitive explanation. I was grateful she did no ask that question.

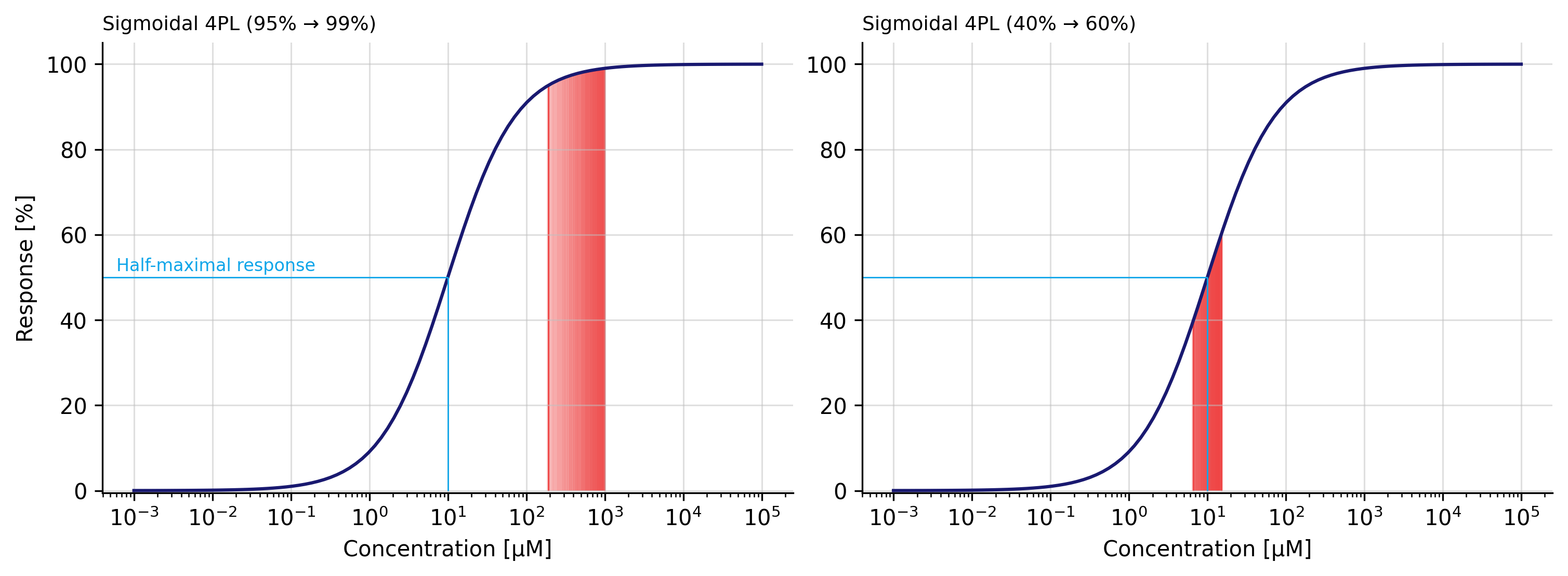
I started by asking "why don't we report full-maximal", and then it clicked. Suppose we have a drug with an half-maximal concentration of 1 µM (indicated in blue), we have these two plots. They are identical; the difference is where we want to compare.

# %% ---------------------------------------------------------------------------
# Load modules
import matplotlib.pyplot as plt
import numpy as np


# %% ---------------------------------------------------------------------------
def cooperative_binding(x, bottom, top, ec50, hill):
    """4PL model with Hill coefficient for cooperative binding"""
    return bottom + (top - bottom) * (x**hill) / (ec50**hill + x**hill)

x = np.logspace(-3, 5, 100)

# return x if y for a 4PL model
# call with:
#   ic90 = xP(_y * top, bottom, top, ic50, slope)
xP = lambda y, bottom, top, ic50, slope: ic50 * ((top - bottom) / (y - bottom) - 1)**(1/slope)


# %% ---------------------------------------------------------------------------
fig, ax = plt.subplots(ncols=2, figsize=(12, 3.75))
fig.subplots_adjust(wspace=0.1)

y = cooperative_binding(x, 0, 100, 10, 1)
ax[0].semilogx(x, y, color="midnightblue")
ax[0].grid(axis="both", color="silver", zorder=-10, linewidth=0.75, alpha=0.5)
ax[0].spines[["top", "right"]].set_visible(False)
ax[0].set_ylabel("Response [%]")
ax[0].set_xlabel("Concentration [µM]")
ax[0].set_title("Sigmoidal 4PL (95% → 99%)", loc="left", fontsize=9)

pct_95 = xP(0.05 * 100, 0, 100, 10, 1)
pct_99 = xP(0.01 * 100, 0, 100, 10, 1)
pct_50 = xP(0.5 * 100, 0, 100, 10, 1)

for x_, y_ in zip([pct_95, pct_99], [95, 99]):
    line_kws_: dict = {"color": "#ef4444", "zorder": -5, "linewidth": 2/3}
    ax[0].vlines(x=x_, ymin=0, ymax=y_, **line_kws_)

for xs in np.linspace(pct_99, pct_95, 100):
    ys = cooperative_binding(xs, 0, 100, 10, 1)
    ax[0].vlines(xs, ymin=0, ymax=ys, color="#ef4444", alpha=0.2, zorder=-10)

ax[0].set_ylim(-0.5, 105)


y = cooperative_binding(x, 0, 100, 10, 1)
ax[1].semilogx(x, y, color="midnightblue")
ax[1].grid(axis="both", color="silver", zorder=-10, linewidth=0.75, alpha=0.5)
ax[1].spines[["top", "right"]].set_visible(False)
ax[1].set_xlabel("Concentration [µM]")
ax[1].set_title("Sigmoidal 4PL (40% → 60%)", loc="left", fontsize=9)

pct_40 = xP(0.60 * 100, 0, 100, 10, 1)
pct_60 = xP(0.40 * 100, 0, 100, 10, 1)

for x_, y_ in zip([pct_40, pct_60], [40, 60]):
    line_kws_: dict = {"color": "#ef4444", "zorder": -5, "linewidth": 2/3}
    ax[1].vlines(x=x_, ymin=0, ymax=y_, **line_kws_)

for xs in np.linspace(pct_60, pct_40, 100):
    ys = cooperative_binding(xs, 0, 100, 10, 1)
    ax[1].vlines(xs, ymin=0, ymax=ys, color="#ef4444", alpha=0.2, zorder=-10)

ax[1].set_ylim(-0.5, 105)

for axn in [0, 1]:
    ax[axn].hlines(y=50, xmin=0, xmax=pct_50, color="#0ea5e9", linewidth=2/3)
    ax[axn].vlines(x=pct_50, ymin=0, ymax=50, color="#0ea5e9", linewidth=2/3)

ax[0].text(s="Half-maximal response", fontsize=8, x=0.0006, y=51.5, color="#0ea5e9")

print(f"IC99 at {pct_99:.2f} µM")
print(f"IC95 at {pct_95:.2f} µM")
print(f"IC60 at {pct_60:.2f} µM")
print(f"IC50 at {pct_50:.2f} µM")
print(f"IC40 at {pct_40:.2f} µM")

fig.savefig("comparison.png", dpi=300, format="png", bbox_inches="tight")
plt.show()

Moving the needle from 95% half-maximal concentration (190 µM) to 99% (990 µM) requires bumping up the concentration by 5.21-fold for a 5% increase in response. Meanwhile, the difference between 40% (6.67 µM) -> 60% (15 µM), a 20% increase in response, requires a more modest 2.25x increase in concentration. This simple observation leads to two conclusions:

• Reaching for full-maximal is costly. The half-maximal concentration is 1 µM, while the full-maximal concentration exceeds 990 µM. To report for EC₉₉ every single time has a terrible value propostion.
• Assay resolution between 40% to 60% is high where a small change in drug concentration is measurable. This two response points sit at the most linear part of the curve. Due to the high resolution, the measurement is more robust and reliable.

Curves modeled by sigmoidal 4PL equation has features that allow for extensive interpretations for a given dose-response observation, of which I will briefly discuss one of them: the maximum value at saturation^[4]. With regard to binding assays (e.g. ELISA), the maximum value (B_max) informs epitopes availability; such that for monoclonal antibody A, the observed B_max of OD=2 whereas monoclonal antibody B has a B_max of OD=3, both are specific to the same antigen. With some assumptions being made (not discussed here), we can probably conclude that monoclonal A can only access 2/3 of epitopes as opposed to monoclonal B.